同态加密与共享协同过滤
本文为系列文章中的第三篇. 言简意赅的说, 同态加密能够让你在不知道我的数据的情况下帮我完成运算.
多方参与的基于协同过滤的推荐系统的需求
基于协同过滤的推荐系统以用户-项目历史评分矩阵为核心, 数据集的容量和特征对最终产生的推荐结果起着至关重要的作用. 正如前文提及, 相较于其他推荐系统, 基于协同过滤的推荐系统存在着对数据集的强依赖以及对新用户或新项目的“冷启动”的弊端. 除此以外, 协同过滤推荐算法的准确性本身也与数据集容量呈正相关趋势. 为了解决基于协同过滤的推荐系统的弊端并进一步提升推荐的准确行, 核心解决思路是获取容量更大, 质量优秀的数据集.
相比于等待自身数据集容量的扩充, 允许分布式环境下的多平台联合参与的协同过滤推荐系统更加直接有效, 即如果淘宝, 京东, 亚马逊如果愿意共享用户购买和评分历史数据的话, 三者的推荐系统准确度都有希望得到巨大的提升. 然而, 出于保护用户隐私, 商业数据隐私等原因, 这些平台不可能向对方公开自己的数据记录.
同态加密
同态加密(Homomorphic Encryption, HE)是一种加密形式, 与其他传统的加密方式的用户不能对密文进行除解密和传输外的任何操作不同, 同态加密允许第三方对密文进行特定的代数运算后得到加密结果, 对加密结果进行解密后得到的值与直接对明文进行同样的运算相同. 同态加密技术的意义在于, 我们放心的将自己数据进行加密后传输给第三方并委托其代理计算, 第三方仅能接触到密文, 因此我们无需担心数据的安全性问题. 同态加密是密码学领域的一个重要课题, 未来会随着云计算的发展拥有更加广阔的前景.
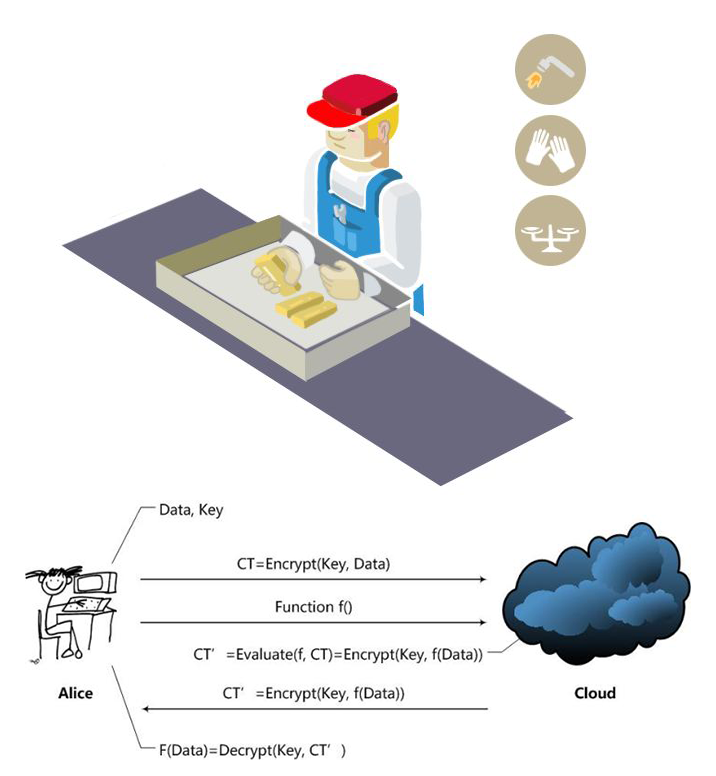
虽然全同态加密已在理论上取得突破, 但其实际计算性能过低, 严重影响实现系统的实际可用性. 因此本文尝试利用在性能上相对更具优势的Paillier同态加密为基于局部敏感哈希的协同过滤的推荐系统实现允许多方保证数据安全的前提下共同参与推荐结果计算.
Paillier同态加密
Paillier同态加密是一种基于和数分解困难性的概率公钥密码系统, 其满足加法同态性质. 此处我们介绍其数学原理, 包含三个部分, 密钥对生成, 加密与解密.
数学原理
- 密钥对生成
- 随机选择两个大素数$p$和$q$, 并保证$p$与$q$相互独立, 即满足$gcd(pq,(q-1)(q-1))=1$.
- 计算$n=pq$, $\lambda =lcm(p-1,q-1)$.
- 随机选择整数$g\in Z_{n^{2}}^{*}$.
- 通过以下计算检查模块化乘法逆元的存在性并确定$n$及$g$的顺序划分: $\mu =(L(g^{\lambda} \mod n^{2})^{2})^{-1}\mod n$, 其中$L(x)=\frac{x-1}{n}$.
- $(n,g)$即为公钥, $(\lambda, \mu)$即为私钥.
- 加密
- 设$m$为明文, 满足$0\leq m<n$.
- 随机选择$r$, 满足$0<r<n$.
- 计算密文: $c=g^{m}\cdot r^{n}\mod n^{2}$.
- 解密
- 设$c$为密文, 满足$c\in Z_{n^{2}}^{*}$.
- 计算明文: $m=L(c^{\lambda}\mod n^{2})\cdot \mu \mod n$.
Paillier算法的加同态性
Paillier同态加密满足加同态性质, 细言之, 若用$E(m)$表示Paillier算法的加密过程, $D(c)$表示Paillier算法的解密过程, 则其满足以下公式:
$$D(E(m_{1},r_{1})\cdot E(m_{2},r_{2})\mod n^{2})=m_{1}+m_{2}\mod n$$
$$D(E(m_{1},r_{1})\cdot g^{m_{2}}\mod n^{2})=m_{1}+m_{2}\mod n$$
$$D(E(m_{1}, r_{1})^{m_{2}}\mod n^{2})=m_{1}m_{2}\mod n$$
$$D(E(m_{2}, r_{1})^{m_{1}}\mod n^{2})=m_{1}m_{2}\mod n$$
利用Paillier同态加密与协同过滤推荐系统结合的可行性
利用Paillier同态加密的性质, 可以实现多平台在不了解明文数据的情况下参与到针对特定用户-项目历史评分数据向量的协同过滤推荐过程中. 根据Paillier同态加密的性质, 不难看出, 如果仅传输使用公钥加密后的密文数据, 参与平台仅能做密文间的求和, 密文与常量间的求和与求积操作. 但回顾我们所使用的相似性度量方法——皮尔逊相关系数的计算方式可以看到, 在其计算过程中涉及原始数据的求积操作, 而第三方平台拿到的密文不支持此操作, 因此, 如果以皮尔逊相关系数作为用户-项目历史评分矩阵上的相似度度量方式, 并且要以Paillier同态加密实现多方参与的数据安全的基于协同过滤的推荐系统的话, 请求参与的平台不仅需要发布待推荐目标个体的历史数据向量, 还应部分参与后续第三方无法完成的计算.
结合过程的实现思路
深入此推荐过程, 则核心问题的定义可以解释为: 若平台$A$使用基于用户的协同过滤推荐系统, 需要针对某一用户-项目历史评分向量$\overrightarrow{m}$进行推荐, 并且为提高推荐的准确度, 请求平台$B$参与推荐结果的计算, 已知或假设平台$A$与$B$间各自拥有不重合的用户群, 但项目相同. 要求平台$A$与平台$B$在各自不向对方和第三方暴露任何自身原始数据的情况下, 平台$B$协助平台$A$共同完成对$\overrightarrow{m}$的推荐结果计算.
为了实现这个过程, 首先平台$A$使用密钥对中的公钥对$\overrightarrow{m}$中的元素进行加密, 发布加密后的密文向量$\overrightarrow{e}$, 并发送至平台$B$. 因为前文在尝试解决基于协同过滤的推荐系统的推荐效率与实时性上使用了局部敏感哈希, 因此假设平台$A$与$B$使用了同样的技术, 因此平台$A$在发布$\overrightarrow{e}$时应当附上其未加密的明文或私钥加密后的索引信息, 否则平台$B$需要遍历其整个数据集. 发布明文或私钥加密后的索引信息意味着平台$B$可以得到$\overrightarrow{e}$在哈希表组中的映射情况, 但这个过程并不涉及数据隐私的泄露, 因为降维后的索引既不包含也不能直接逆推用户或项目的原始评价信息. 这里又分为两种情况, 若平台$A$及平台$B$的局部敏感哈希表使用了前文所述的技术生成, 并且使用的时相同的随机向量组, 则此时平台$A$仅需直接发布$\overrightarrow{e}$在自身哈希表组中的索引值. 但更常见的是双方的哈希表组各自使用不同的随机向量组生成, 则此时平台$B$为了得到正确的索引信息, 需要向$A$提供自己的随机向量组并请求$A$计算出对应的索引, 同样, 此过程不涉及任何用户数据, 对用户数据的安全性没有影响. 除此之外, 注意到我们采用的皮尔逊相关系数的计算过程中包含求原数据乘方和的过程, 但Paillier同态加密不具备乘同态性, 无法完成此操作, 因此在发布密文向量时, 需要同时发布密文向量标准化后的对应的密文向量和该向量乘方和的密文值, 补充内容仅为$B$能够完成其协同过滤计算过程中的基于皮尔逊相关系数的相似度的计算, 使其计算过程仅包含加法, 此补充内容全部为公钥加密后的密文, 平台$B$仍然无法得到任何与用户明文数据相关的信息.
平台$B$在拿到平台$A$发布的请求及密文数据后, 首先利用索引信息找到近似近邻用户群参与接下来的计算, 使用密文用户-项目历史评分向量$\overrightarrow{e}$与近似近邻用户群中的用户向量计算皮尔逊相关系数. 由于标准化后的密文向量及其乘方和的密文已被平台$A$一起提供, 因此求皮尔逊相关系数的操作除最后一步意外仅剩求和操作, 由Paillier算法的加同态性易知, 此过程可以得到正确的结果. 在皮尔逊相关系数计算的最后一步, 即求协方差与标准差成绩的比值时, 由于Paillier算法不具备乘同态性, 因此分子和分母的计算结果需要回传值平台$A$进行最终计算, 回传过程为保证数据不被第三方获取, 可用平台$A$的公钥加密. 此过程中, 虽然分子和分母被回传至平台$A$后可以被平台$A$解密得到原始明文, 但作为汇总求和的单值结果, 既不包含也无法直接逆推任何平台$B$的用户-项目评分原始数据. 此过程最终得到了相似度计算结果. 此后对相似度结果排序, 按照协同过滤算法的方式计算出对应的评分预测向量的分子和分母, 并将结果回传至平台$A$, 平台$A$得到计算结果后与自身计算结果合并的到最终结果.
推荐系统的结构和流程可以用下图表示:
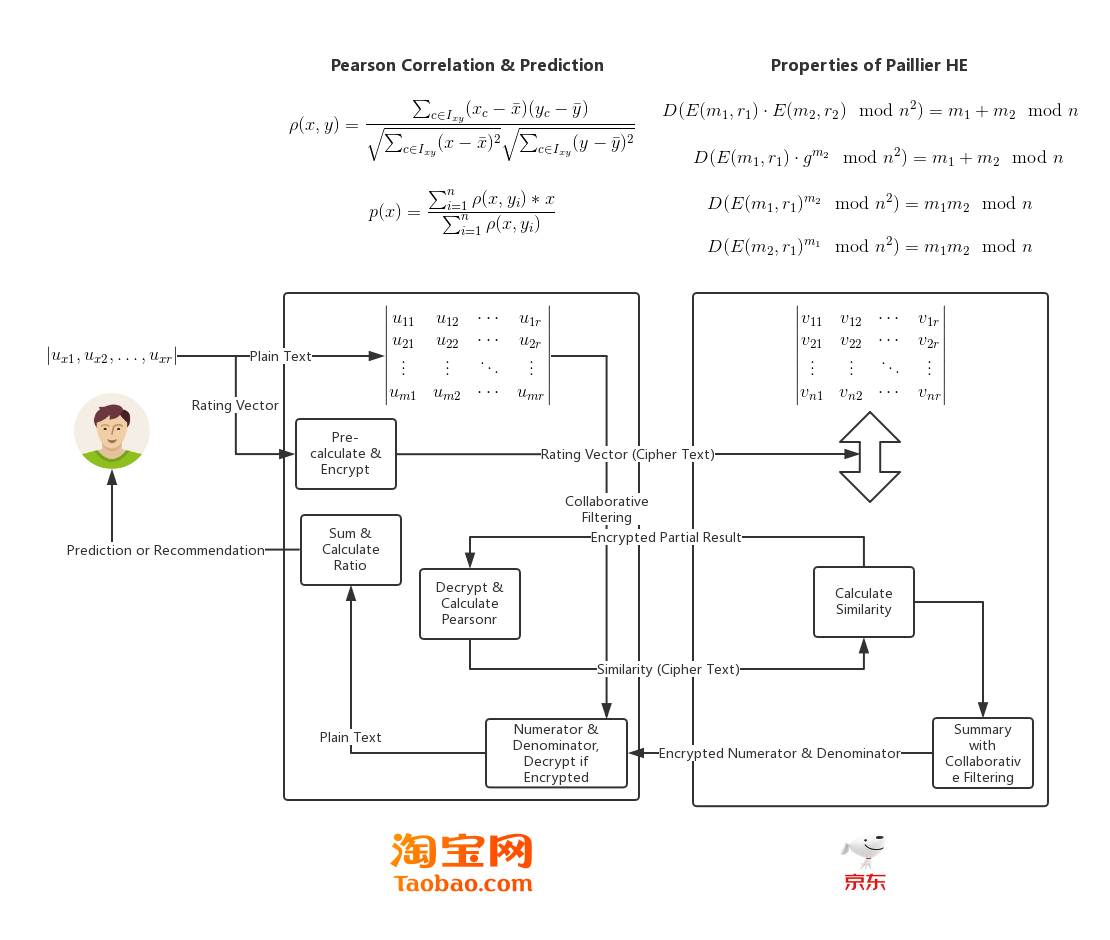
观察此流程图, 回顾整个系统实现, 计算请求方与参与方间的通信仅包含用户评分数据向量及相关计算结果的密文, 局部敏感哈希表组索引情况以及最终的汇总计算结果, 不包含双方自身用户-项目评分矩阵内的任何信息及待推荐用户的评分信息. 计算完成后, 参与方无法得知推荐目标用户的评分, 因此请求方保护了用户及企业数据隐私, 而请求方也不能从汇总结果中逆推参与方用户-项目评分将矩阵的情况, 参与方的数据安全性得以保证.
伪代码实现
整个过程用Python伪代码可以表示为:
public_key, private_key = paillier.generate_paillier_keypair()
encrypted_user_vec = [public_key.encrypt(i) for i in user_vec]
sum_of_similarity, sum_of_ratings_with_weights = cacl_using_self_data()
hash_table_indexes = get_hashtable_indexes(user_vec)
for platform in subscribers:
x, y = platform.participate(encrypted_user_vec, hash_table_indexes, self)
sum_of_ratings_with_weights += np.array([self._private_key.decrypt(i) for i in x])
sum_of_similarity += private_key.decrypt(y)
result = sum_of_ratings_with_weights / sum_of_similarity其中, participate为调用请求平台协助参与计算, 其实现可以用Python伪代码表示为:
collection = get_similar_collection(hash_table_indexes)
similarities = np.empty((len(collection),))
for i, user_vec in enumerate(collection):
similarities[i] = calc_similarity_with_encrypted_data(user_vec, encrypted_user_vec, platform)
most_similar_indexes = platform.encrypted_data_argsort(similarities)[0 - k:]
_, items_count = data.shape
sum_of_similarity, sum_of_ratings_with_weights = 0, [0 for _ in range(items_count)]
for index in most_similar_indexes:
sum_of_similarity += similarities[index]
for i, value in enumerate(collection[index]):
sum_of_ratings_with_weights[i] += similarities[index] * value
result = (sum_of_ratings_with_weights, sum_of_similarity)其中calc_similarity_with_encrypted_data为计算明文向量与经过Paillier同态加密算法加密后的密文向量间的皮尔逊相关系数, 其实现与普通的皮尔逊相关系数的区别仅在于以同态加替换原始求和, 并将协方差与标准差乘积求商的过程委托至原平台完成.
实验及分析
基于同态加密与局部敏感哈希的协同过滤推荐系统的安全性已在前文论证, 接下来我们实际测试此系统推荐结果的准确度和性能指标. 本实验在与局部敏感哈希实验的硬件条件相同的情况下, 考虑到同态加密的性能需求, 适当降低数据集规模至256个用户, 36部电影. 实验中训练集与测试集比例9: 1, 假设每个平台占有的数据量为整个训练集的50%. 针对单平台的协同过滤推荐, 多平台基于Paillier同态加密的协同过滤推荐, 在运行时间和运行结果平均绝对误差做评估, 重复实验64次并取平均值, 得到到以下结果:
| Time Using HE(ms) | Time NOT Using HE(ms) | MAE Using HE | MAE NOT Using HE |
|---|---|---|---|
| 160072.25 | 245.0 | 0.4221464289286429 | 0.45617146643385553 |
从实验结果可以看到, 在使用同态加密后, 由于更多数据参与推荐结果的计算, 平均绝对误差得以下降, 即推荐的准确率的到了提升. 但由于计算过程中使用同态加密带来了大量额外开销, 因此性能下降幅度较为明显.
总结
至此的三篇博文已经把我的论文主体内容讲述完了, 对应的项目代码和论文原文可以在GitHub上查看. 我个人水平比较有限, 文中若存在错误或者大家对此有什么疑问可以通过我在关于页面中留下的联系方式与我讨论. 最近忙于毕业和工作的事, 学生时代的暂时结束也是让人感慨颇多, 愿你我在未来的时光里砥砺前行, 共同进步.
许可协议: CC BY-NC-SA 4.0
本文链接:https://blog.angelmsger.com/同态加密与共享协同过滤/