利用局部敏感哈希改进推荐系统实时性 | 齐浩天的博客

本文为系列文章中的第二篇. 局部敏感哈希与我曾经在上一篇文章中提到过的相似哈希比较类似, 把高维空间中相近的点映射到哈希表中相同的桶中.

传统的基于协同过滤的推荐系统在实时性方面的弊端

面对具有大规模高维稀疏矩阵特征的用户-项目历史评分矩阵, 传统的单纯的基于协同过滤的推荐系统存在计算量大, 扩展性不强, 推荐效率低等问题, 严重影响实时推荐系统的实现, 因此本文尝试在现有基于协同过滤的推荐系统上, 引入局部敏感哈希(Local-Sensitive-Hashing, LSH)对其进行改进, 局部敏感哈希基于随机映射机制将高维空间的数据降维, 并原空间中距离较近的两个点在映射后距离仍以极大概率保持接近. 这种相似性不是精确保证的, 但在实际应用中能够很大程度满足实现的需求.

局部敏感哈希

核心思想

局部敏感哈希的核心思想是选择一种可以将原空间中相似对象以极高概率映射或投影到同一桶中的哈希函数, 通过这种映射, 大量极大概率不相近的个体被过滤掉, 因此在求近邻用户群时无需遍历整个数据集, 降低了相似性计算的代价. 由于局部敏感哈希本身是一种基于概率的模型, 因此在实现时通常会创建多个哈希表, 并在求近似近邻数据集时以所有哈希表返回结果的并集作为最终结果. 实践证明, 局部敏感哈希在数据规模与维度较大的稀疏矩阵下具有良好的相似性检索性能. 此外, 后文中还将提及, 在多方参与的基于协同过滤的推荐系统中, 暴露局部敏感哈希生成的索引本身是相对安全的, 因为降维后的数据并不直接泄露数据隐私. 其主要思想可以通过下图表示:

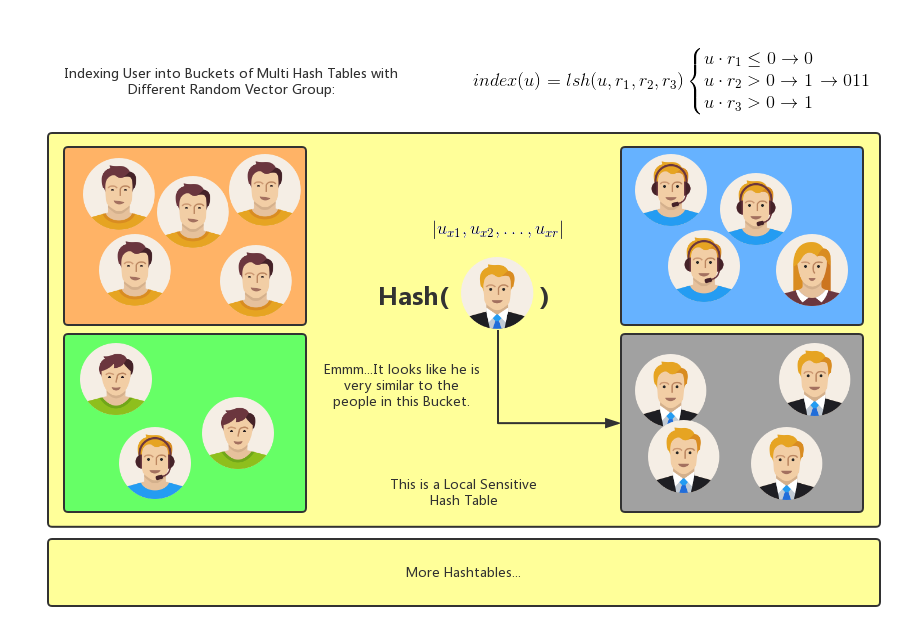
数学定义

局部敏感哈希的严格定义如下: 设某度量空间$R^{d}$下的哈希函数族$H$, 该函数族是$R^{d}$中点域$S$到某个集合域$D$的一组哈希函数, 任选哈希函数$h_{i}$对$R^{d}$内数据点$a$和$b$进行哈希, 若其满足:

1. 若$\left | a-b \right |\leq r_{1}$, 则$Prob[h_{i}(a)=h_{i}(b)]\geq p_{1}$;
2. 若$\left | a-b \right |\geq r_{1}$, 则$Prob[h_{i}(a)=h_{i}(b)]\leq p_{2}$.

其中$Prob[\cdot ]$为概率函数, $0<r_{1}\leq r_{2}$, $0\leq p_{1}<p_{2}\leq 1$, 则此哈希函数族称为$(r_{1},r_{2},p_{1},p_{2})$-位置敏感哈希函数族.

任一用户-项目评分向量经过位置敏感哈希函数映射到对应桶中, 则同一桶中的其他向量组成的集合可被视为近似近邻目标群. 由于局部敏感哈希本身是一种基于概率的模型, 因此在实现时通常会创建多个哈希表, 因此需要将多个哈希表中的与目标用户-项目评分向量处于同一统中的全部其他向量取并集作为最终的近似近邻目标群.

实现方式

在与基于协同过滤的推荐系统相结合的具体实现中, 推荐过程分为3个部分: 其一, 离线建立用户索引, 此过程即对用户-项目历史评分矩阵中的每一个用户或项目向量进行哈希映射, 存入哈希表; 其二, 在线查找相似用户, 此过程即将被推荐的目标向量以相同的哈希函数映射入每个哈希表的某一桶, 并将同一桶中的其他向量取出取并集作为近似近邻目标群; 其三, 推荐, 此过程即以得到的近似近邻目标群为数据集, 运行协同过滤推荐算法, 得到推荐结果. 由于最终的推荐仅需遍历得到的近似近邻目标群, 而此群体容量通常比整个数据集的容量小若干个数量级, 因此可以极大的提升推荐的实时性.

离线建立索引

具体到局部敏感哈希离线建立索引过程中的哈希函数的选择, 需要基于前文中对于局部敏感哈希函数的定义, 并且与所使用的相似度度量方式有关. 本文实现使用的是运用较为广泛的皮尔逊相关系数, 因此给出皮尔逊相关系数对应的局部敏感哈希函数事项方式.

以基于用户的协同过滤推荐系统为例, 一个用户的历史评分向量可以表示为一个$n$维向量$\overrightarrow{u}=(u_{1},u_{2},…,u_{n})$, 其中$u_{i}$为用户对第$i$个项目的评分, 此时新建随机$n$维向量$\overrightarrow{v}=(v_{1},v_{2},…,v_{n})$, 其中$v_{n}$为$[-1,1]$内的随机数. 设哈希函数族$H=(h_{1},h_{2},…,h_{m})$, 其中$h_{i}$为:

$$f(\overrightarrow{u})=\begin{cases}1, &\overrightarrow{u}\cdot \overrightarrow{v}>0\ 0, &\overrightarrow{u}\cdot \overrightarrow{v}\leq 0\end{cases}$$

通过一个哈希函数族$H$内的一个哈希函数$h_{i}$和一个随机向量$\overrightarrow{v}$, 一个$n$维用户-项目历史评分向量被映射为一个二进制值0或1. 将哈希函数族内的$m$个哈希函数(同一哈希算法对应不同的随机向量$\overrightarrow{v}$)按照以上方式应用于用户-项目历史评分向量, 则可以得到一个$m$维二进制向量, 即我们通过以上局部敏感哈希操作, 将$n$维用户-项目历史评分向量映射为一个$m$维二进制向量(或其表示的整数值), 而映射结果相同的原始用户-项目历史评分向量有极大可能性相似. 如前文所述, 由于局部敏感哈希本身是一种基于概率的模型, 因此在实现时通常会创建多个哈希表, 但每个哈希表的实现方式都是相同的, 只是采用随机向量不同.

伪代码实现

若用$M$表示原始用户-项目历史评分矩阵, $t$表示建立哈希表数量, 则建立离线索引的过程可以用以下Python伪代码表示:

users_size, items_size = M.shape
hashtables = [[[]] for _ in range(int('1' * m) + 1)] for _ in range(t)]
random_matrixes = [np.empty((m, item_size)) for _ in range(t)]
for i, user_vec in enumerate(M):
    for j in range(t):
        v = random_matrixes[i, j] = np.random.uniform(m, items_size, (-1, 1))
        index = ''
        for k in range(m):
            index += '1' if user_vec.dot(v[k]) > 0 else '0'
        hashtables[j].append(i)

在线查找相似用户

在在线查找相似用户时, 不再需要遍历整个数据集, 依次求得全部相似度并排序, 而是直接计算其在每个哈希表中对应的桶编号, 并将这些桶中的所有用户-项目历史评分向量取出作为目标用户的近似近邻用户群. 仅需遍历此近似近邻用户群, 依次求得与目标的相似度后排序, 即可得到真实的“K-最近邻”用户群, 参与后续的协同过滤推荐计算.

伪代码实现

若用$target_vec$表示待推荐的目标用户-项目历史评分向量, 此在线查找相似用户的过程可以用以下Python伪代码表示为:

sililar_users = set()
for i, hashtable in enumerate(hashtables):
    index = ''
    for j in range(m):
        index += '1' if target_vec.dot(random_matrixes[i, j]) > 0 else '0'
    index = int(index, 2)
    sililar_users |= hashtable(index)

实验及分析

运用相似敏感哈希技术改进的基于协同过滤的推荐系统在一定程度上解决了推荐的实时性差的弊端, 提高了查找效率, 满足了快速相应的需求, 接下来, 我们讨论如何在保证数据隐私安全的情况下, 允许多方共同参与协同过滤推荐, 减小基于协同过滤的推荐系统在数据集大小方面的限制.

实验结果使用基于以下实验环境:

CPU	RAM	OS	LANG
i7-4720HQ	16GB DDR3	Arch Linux(with Kenel 4.16.8-1)	Python 3.6.5

数据集使用MovieLens, 该数据集收集了700个用户对9000部电影的评分记录. 推荐结果质量评估标准使用平均绝对误差(Mean Absolute Error, MAE), 其值越小, 代表推荐结果越准确. 若用$\overrightarrow{p}$表示对用户预测的评分向量中的用户已有历史记录, $\overrightarrow{u}$表示用户产生的真实评分向量, $t$表示向量长度, 则$MAE$可以表示为: $$MAE=\frac{\sum_{i=1}^{t}\left | p_{i}-u_{i} \right |}{t}$$

下表为使用局部敏感哈希改进后的协同过滤推荐系统在不同数据集容量情况下的8次推荐计算过程中平均话费时间对比, 单位为微秒, 以及平均绝对误差对比:

Size of Dataset	Time Using LSH(ms)	Time NOT Using LSH(ms)	MAE Using LSH	MAE NOT Using LSH
37	334.91176471	2804.61764706	0.41670966	0.31702144
74	421.44117647	5173.89705882	0.30188026	0.19453976
111	547.01470588	7727.47058824	0.2932903	0.19527124
148	624.27941176	10202.52941176	0.31379263	0.19609297
185	707.44117647	12621.91176471	0.30687005	0.19651358
222	752.	15062.51470588	0.28993342	0.19611309
259	813.85294118	17499.91176471	0.28989946	0.19616549
296	891.94117647	20082.41176471	0.27720024	0.1962684
333	941.32352941	22265.94117647	0.27661047	0.19624015
370	1010.01470588	24715.38235294	0.25593213	0.15414695
407	1048.77941176	27198.45588235	0.26337683	0.1539606
444	1118.32352941	29728.79411765	0.25759909	0.15398098
481	1210.32352941	32366.79411765	0.23178155	0.15373239
518	1255.95588235	34337.86764706	0.23679564	0.15389964
555	1378.19117647	37129.05882353	0.24840943	0.15402475
592	1425.47058824	39571.48529412	0.17902636	0.1

或如下图:

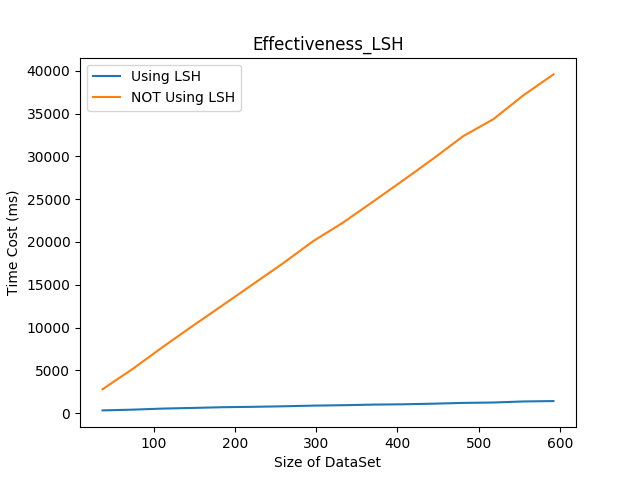
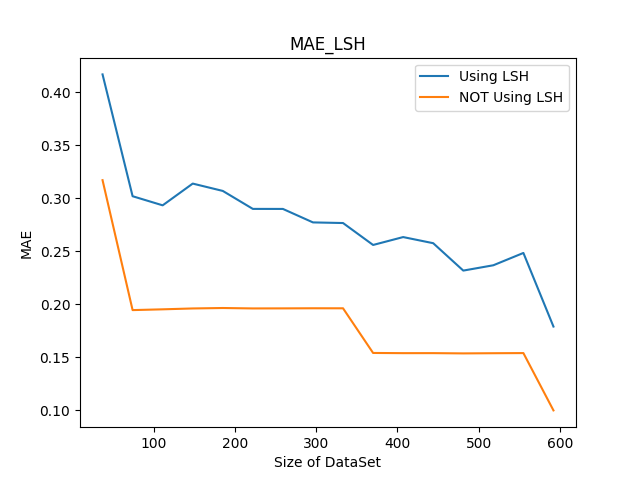
根据实验结果可以看出, 在使用局部敏感哈希改进基于协同过滤的推荐系统后, 计算效率得到了非常显著的提升, 同时推荐质量也没有因此受到较大的影响.

基于局部敏感哈希的隐私保护

局部敏感哈希不仅能够避免不必要的计算, 提升推荐结果计算效率, 同样可以作为多方参与的基于协同过滤的推荐系统中的一种数据隐私保护方式. 降维后的用户评分数据向量索引本身不包含且不可逆推用户的实际打分, 因此若以最简单的方式考虑, 则可以提出一种仅基于局部敏感哈希的允许多方参与的基于协同过滤的推荐系统实现, 即当请求计算推荐结果的目标用户到达时, 根据哈希函数计算出其索引值, 并将索引值发送给参与方, 参与方依据此索引分别从所有哈希表中取出所有近似近邻元素, 计算其非零评分平均值作为结果返回至请求方, 请求方拿到结果后与基于自身的运算结果合并, 求出最终结果.

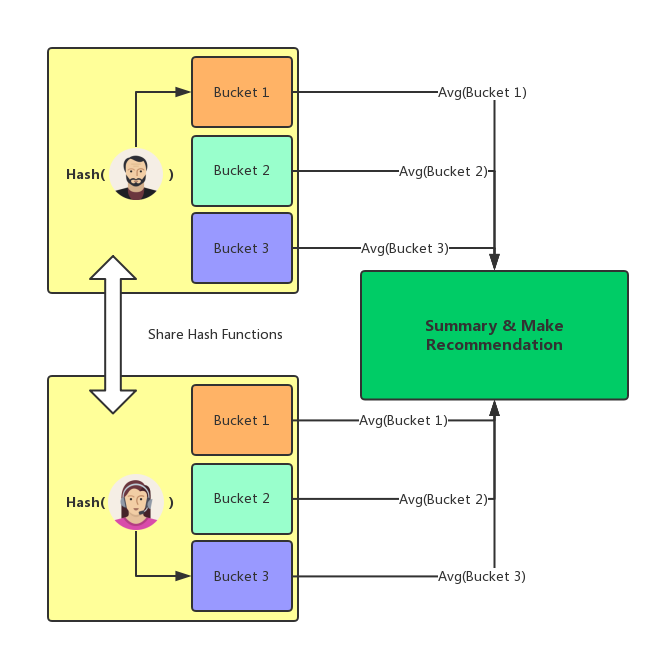
这种方式实现起来非常简单, 本文不再展开叙述, 其传输过程也仅涉及索引值, 安全性能够保证. 但同样也可以看出, 这种实现方式不考虑向量间相似度大小的具体差异, 其推荐结果的准确度相对较低. 为了实现明确相似度的度量以及以此为基础的协同过滤推荐系统, 下一篇文章考虑引入同态加密.

许可协议: CC BY-NC-SA 4.0
本文链接：https://blog.angelmsger.com/利用局部敏感哈希改进推荐系统实时性/